symmetrische GruppeDefinition symmetrische Gruppe
Universität
In der Halbgruppe 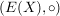 aller Abbildungen einer Menge aller Abbildungen einer Menge 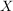 in sich (mit der Komposition von Abbildungen als Verknürpfung, in sich (mit der Komposition von Abbildungen als Verknürpfung, 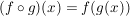 , ist , ist 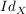 neutrales Element und die bijektiven Abbildungen, also die Permutationen von neutrales Element und die bijektiven Abbildungen, also die Permutationen von 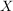 , sind genau die invertierbaren Elemente in , sind genau die invertierbaren Elemente in 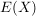 . Also ist . Also ist
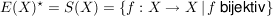
zusammen mit der Komposition von Abbildungen eine Gruppe.
Sie heißt die Gruppe der Permutationen von 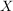 oder die symmetrische Gruppe von oder die symmetrische Gruppe von 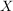 . .
Für den wichtigen Spezialfall 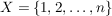 setzen wir setzen wir
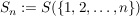 . .
Die Elemente von 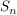 heißen Permutationen __vom Grad heißen Permutationen __vom Grad  , sie werden häufig in der Form , sie werden häufig in der Form
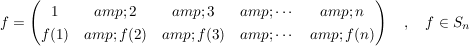 angegeben. Schreibt man
angegeben. Schreibt man 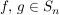 in dieser Form, dann erhält man für das Produkt in dieser Form, dann erhält man für das Produkt 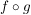
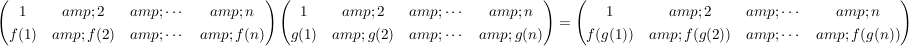 .
Man fängt also die Auswertung beim rechten Faktor an, so wie es sich für ein Produkt von Abbildungen auch gehört.
Beispiel .
Man fängt also die Auswertung beim rechten Faktor an, so wie es sich für ein Produkt von Abbildungen auch gehört.
Beispiel
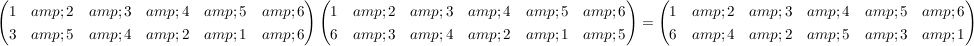 .
Man geht nach dem Schema vor: .
Man geht nach dem Schema vor:
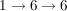 , ,
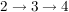 , ,
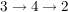 ,
etc.
(" ,
etc.
("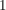 wird auf die wird auf die 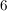 abgebildet, dann bleibt abgebildet, dann bleibt 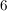 fest, insgesamt fest, insgesamt 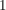 auf auf 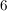 ; ; 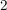 wird auf wird auf 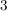 abgebildet, dann abgebildet, dann 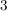 auf auf 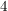 , insgesamt , insgesamt 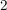 auf auf 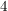 , etc.")
Das Inverse , etc.")
Das Inverse 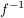 von von 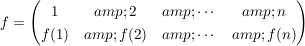 ist die Abbildung ist die Abbildung
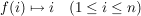 ,
d.h. wir vertauschen in ,
d.h. wir vertauschen in 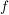 die Zeilen, erhalten die Zeilen, erhalten
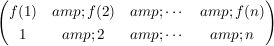 und bringen dies in die richtige Reihenfolge, so dass wir in der oberen Zeile die natürliche Anordnung haben. Das Ergebnis ist
und bringen dies in die richtige Reihenfolge, so dass wir in der oberen Zeile die natürliche Anordnung haben. Das Ergebnis ist 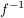 .
Beispiel .
Beispiel
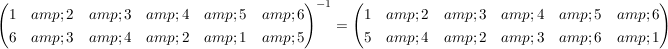 .
Es gilt: .
Es gilt: 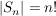 .
__Beweis (Induktion): .
__Beweis (Induktion): 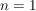 ist klar. Die Zahl ist klar. Die Zahl  kann in der zweiten Zeile einer Permutation aus kann in der zweiten Zeile einer Permutation aus 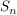 an an  verschiedenen Stellen vorkommen, nämlich unter verschiedenen Stellen vorkommen, nämlich unter 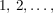 oder oder  . Für jede dieser . Für jede dieser  Möglichkeiten können die restlichen Möglichkeiten können die restlichen 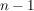 Zahlen auf Zahlen auf 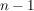 Stellen verteilt werden. Dafür gibt es nach Induktionsvoraussetzung Stellen verteilt werden. Dafür gibt es nach Induktionsvoraussetzung 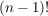 Möglichkeiten. Insgesamt haben wir daher Möglichkeiten. Insgesamt haben wir daher 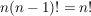 Möglichkeiten, die Zahlen Möglichkeiten, die Zahlen 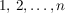 in verschiedene Reihenfolgen zu bringen. in verschiedene Reihenfolgen zu bringen.
Fortsetzung folgt später...
Quelle: isbn3446130799
| 