ÄquivalenzumformungVersion 4 von Mi 05.01.2005 um 17:24(Unterschied) ← Nächstältere Version | Aktuelle Version ansehen| Nächstjüngere Version → (Unterschied) Gegeben sei ein Lineares Gleichungssystem durch
(1) 2x + 3y = 15,5
(2) 5x - 2y = 5,5
Dann kann man unter drei Lösungsverfahren wählen:
Geichsetzungsverfahren
Man löst beide Gleichungen nach derselben Variablen auf und setzt die beiden rechten Seiten der Gleichungen gleich (weil ja links auch dasselbe steht).
Dadurch erhält man eine (lineare) Gleichung mit nur einer Variablen, die man wie gewohnt lösen kann. Anschließend berechnet man aus einer der gegebenen Gleichungen die 2. Variable und macht mit der anderen Gleichung die Probe. (wichtig!)
Einsetzungsverfahren
Aus einer der beiden Gleichungen wird eine Variable freigerechnet. Diesen Ausdruck setzt man in die andere Gleichung ein und löst die so entstehende (lineare) Gleichung wie gewohnt und macht mit der ersten Gleichung die Probe. (wichtig!)
Additionsverfahren
Man erreicht durch geeignete Multiplikation der Gleichungen, dass die Koeffizienten einer Variablen gleich oder umgekehrt gleich sind. Man addiert oder subtrahiert die beiden Gleichungen und erhält so eine (lineare) Gleichung mit einer Variablen, die man wie gewohnt lösen kann. Anschließend berechnet man aus einer der gegebenen Gleichungen die 2. Variable und macht mit der anderen Gleichung die Probe. (wichtig!)
Diese Verfahren eignen sich für Gleichungssysteme mit wenigen Variablen.
Muss man größere Gleichungssysteme lösen, werden die ersten beiden Verfahren leicht unübersichtlich und damit fehlerträchtig.
Stattdessen setzt man dann den Gauß-Algorithmus ein, der ein organisiertes Additionsverfahren darstellt.
Beispiel:
(1) 2x + 3y = 15,5
(2) 5x - 2y = 5,5
Geichsetzungsverfahren
aus (1): x = -1,5y + 7,75
und (2): x = 0,4y + 1,1
folgt: -1,5y + 7,75 = 0,4y + 1,1
y = 3,5
in (1): x = -1,5*3,5 + 7,75 = 2,5
Die Lösungsmenge ist 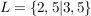
Einsetzungsverfahren
aus (1): x = -1,5y + 7,75
in (2): 5(-1,5y + 7,75) - 2y = 5,5
-7,5y + 38,75 - 2y = 5,5
-9,5y = -33,25
y = 3,5
weiter wie oben...
Additionsverfahren
(1) 2x + 3y = 15,5 | * 5
(2) 5x - 2y = 5,5 | * (-2)
(1.1) 10x + 15y = 77,5
(2.1) -10x + 4y = -11
Addition der Gleichungen:
(1.2) 19y = 66,5
y = 3,5
weiter wie oben ...
::nicht vergessen: Die Probe wird immer an den Ausgangsgleichungen gemacht! ::
Bemerkung
Enthält eine Gleichung einen Wurzelausdruck, so kann man die Gleichung zwar quadrieren
und dann nach der Lösung suchen; aber dieses ist keine Äquivalenzumformung!
Das bedeutet, dass durch dieses Verfahren u.U. zusätzliche Lösungen entstehen.
Darum muss man nach einer solchen Umformung unbedingt
die gefundenen "Lösungen" an der Ausgangsgleichung überprüfen.
Beispiel:
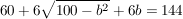 |-60-6b |-60-6b
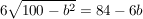 |:6 |:6
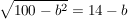 |quadrieren |quadrieren
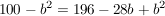 |+b²-100 |+b²-100
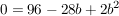 |:2 |:2
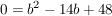 pq-formel pq-formel
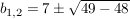
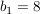
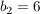
Probe:
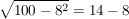
6=6, also ist 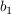 eine Lösung eine Lösung
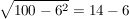
8=8, also ist auch 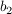 eine Lösung der Gleichung. eine Lösung der Gleichung.
|