Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| Lineare Algebra I/II,
Vorkurs, | www.matheraum.de
Lineare Algebra
Aufgabenblatt 4
Abgabe: Mo 05.03.2012 10:00 | 27.02.2012 | | Die Übungsaufgaben beziehen sich auf das Buch "Lineare Algebra" von Gerd Fischer bzw. auf das Inhaltsverzeichnis, das in der Kursbeschreibung zu finden ist. Die Übungsaufgaben (i.d.R. zu immer einem neuen Kapitel im Buch) können bequem in einer Woche gelöst werden. | | Für diese Serie sollten Sie mit folgenden Begriffen vertraut sein: Vektorraum, Unterraum, Familie von Vektoren, aufgespannter/erzeugter Unterraum (span(M) bzw span(v1,...,v_n)), Linearkombination, Lineare Hülle, Lineare (Un-)Abhängigkeit. | | Aufgabe 1 | IV-1: a) Ist die Menge U:={ 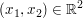 ; ; 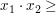 0 } ein Unterraum von 0 } ein Unterraum von 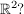
b) Zeigen Sie, dass der Durchschnitt (auch unendlich vieler) Unterräume eines Vektorraums wieder ein Unterraum von V ist. Gilt dies auch für die Vereinigung? | | Aufgabe 2 | IV-2: Zeigen Sie, dass die Menge ![$ C_{[a,b]} $ $ C_{[a,b]} $](/teximg/8/6/01936368.png) aller stetigen Funktionen f: aller stetigen Funktionen f: ![$ [a,b]->\IR $ $ [a,b]->\IR $](/teximg/9/6/01936369.png) ein Unterraum des Vektorraums ein Unterraum des Vektorraums ![$ \IR_{[a,b]} $ $ \IR_{[a,b]} $](/teximg/0/7/01936370.png) aller auf [a,b] definierten reellwertigen Funktionen ist. ( aller auf [a,b] definierten reellwertigen Funktionen ist. ( 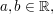 a<b ) a<b ) | | Aufgabe 3 | IV-3: a) Untersuchen Sie, ob sich x= 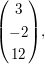 y= y=  und z= und z=  als Linearkombination von u= als Linearkombination von u=  und w= und w=  im im 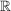 - Vektorraum - Vektorraum  darstellen lassen. darstellen lassen.
b) Untersuchen Sie auf lineare Unabhängigkeit:
(i) im Vektorraum V = 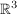 über Körper K = über Körper K = 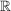 : x= : x= 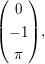 y= y=  und z= und z= 
(ii) im Vektorraum V = 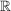 = Körper K: x = 1, y = = Körper K: x = 1, y = 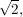 z = z = 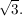
Ändert sich die Lösung, wenn man stattdessen den Körper 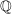 betrachtet? betrachtet? | | Aufgabe 4 | IV-4: Sei V der 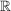 - Vektorraum aller reellwertigen Funktionen f: - Vektorraum aller reellwertigen Funktionen f: 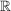 -> -> 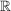 . Zeigen Sie die lineare Unabhängigkeit der folgenden Funktionen aus V: . Zeigen Sie die lineare Unabhängigkeit der folgenden Funktionen aus V:
(a) f(x) = 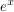 , g(x) = sin(x) , h(x) = , g(x) = sin(x) , h(x) = 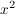
(b) f(x) = 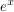 , g(x) = , g(x) = 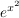 , h(x) = x , h(x) = x
(c) f(x) = 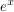 , g(x) = sin(x) , h(x) = cos(x) , g(x) = sin(x) , h(x) = cos(x) |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|
