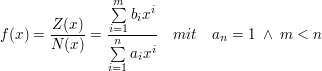Entwicklungssatz nach HeavisideDefinition
Bezugnehmend auf die Partialbruchzerlegung und in Anlehnung an das Residuenkalkül erfolgt hier Erläuterung zur Koeffizentenbestimmung
Sei 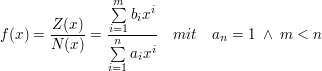
Unter der Voraussetzung, dass
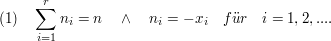
lässt sich das Nennerpolynom N(x) als Produkt darstellen
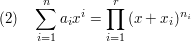
Die zugehörige Partialbruchzerlegung lautet nun:
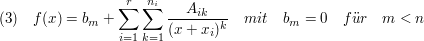
Es gilt nach dem Residuensatz
![$ (4)\quad A_{ik}\ =\ \limes_{x\rightarrow -x_i}\ \bruch{1}{(n_i-k)!}\bruch{d^{n_i-k}}{dx^{n_i-k}}\big[(x-x_i)^{n_i}\cdot{}f(x))\big] $ $ (4)\quad A_{ik}\ =\ \limes_{x\rightarrow -x_i}\ \bruch{1}{(n_i-k)!}\bruch{d^{n_i-k}}{dx^{n_i-k}}\big[(x-x_i)^{n_i}\cdot{}f(x))\big] $](/teximg/0/0/01389400.png)
Das war bis hierher der theoretische Part, nun folgen einige einfache Beispiele, anhand derer die Formel angewendet und erklärt wird. Die Ableitungen, sofern von Nöten, werden ausnahmslos mit der Quotientenregel durchgeführt und jeweils der erste Zwischenschritt notiert (vereinfachte Darstellung):
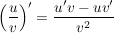
Um die Lesbarkeit zu erhöhen oder Stellen, welche gerade bearbeitet werden müssen, hervorzuheben, werden zunächst verschiedene Farben eingesetzt, auf die immer wieder zurückgegriffen wird
![$ A_{ik}\ =\ \limes_{x\rightarrow -\blue{x_i}}\ \bruch{1}{(\red{n_i}-\green{k})!}\bruch{d^{\red{n_i}-\green{k}}}{dx^{\red{n_i}-\green{k}}}\big[(x-\blue{x_i})^{\red{n_i}}\cdot{}\color{Black}f(x))\big] $ $ A_{ik}\ =\ \limes_{x\rightarrow -\blue{x_i}}\ \bruch{1}{(\red{n_i}-\green{k})!}\bruch{d^{\red{n_i}-\green{k}}}{dx^{\red{n_i}-\green{k}}}\big[(x-\blue{x_i})^{\red{n_i}}\cdot{}\color{Black}f(x))\big] $](/teximg/6/5/01389456.png)
Beispiele
 : Es liegt eine gebrochen-rationale Funktion vor, dessen zwei reelle Nullstellen im Nennerpolynom einfach vorhanden sind (vgl. Artikel: Partialbruchzerlegung): : Es liegt eine gebrochen-rationale Funktion vor, dessen zwei reelle Nullstellen im Nennerpolynom einfach vorhanden sind (vgl. Artikel: Partialbruchzerlegung):
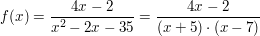
Nach (3) gilt erst einmal:
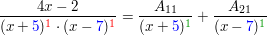
Nach (4) gilt zunächst für 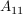 : :
![$ A_{11}\ =\ \limes_{x\rightarrow -5}\ \bruch{1}{({\red{1}}-\green{1})!}\bruch{d^{\red{1}-\green{1}}}{dx^{\red{1}-\green{1}}}\left[(x+\blue{5})^{\red{1}}\cdot{}\left(\bruch{4x-2}{(x+\blue{5})\cdot{}(x-7)}\right)\right] $ $ A_{11}\ =\ \limes_{x\rightarrow -5}\ \bruch{1}{({\red{1}}-\green{1})!}\bruch{d^{\red{1}-\green{1}}}{dx^{\red{1}-\green{1}}}\left[(x+\blue{5})^{\red{1}}\cdot{}\left(\bruch{4x-2}{(x+\blue{5})\cdot{}(x-7)}\right)\right] $](/teximg/5/3/01398135.png)
Das schaut noch alles etwas unübersichtlich aus, jedoch ist 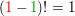 und mit und mit 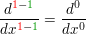 wird die Ableitung nicht gebildet. Zu guter Letzt kann der Teil in den eckigen Klammern noch vereinfacht werden, da sich (x+5) herauskürzt. Es bleibt übrig: wird die Ableitung nicht gebildet. Zu guter Letzt kann der Teil in den eckigen Klammern noch vereinfacht werden, da sich (x+5) herauskürzt. Es bleibt übrig:
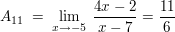
Für die Bestimmung von 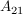 wird natürlich das gleiche Prinzip angewendet wird natürlich das gleiche Prinzip angewendet
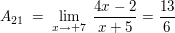
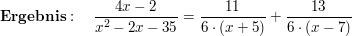
 : Es liegt eine gebrochen-rationale Funktion vor, dessen drei reelle Nullstellen im Nennerpolynom einfach vorhanden sind: : Es liegt eine gebrochen-rationale Funktion vor, dessen drei reelle Nullstellen im Nennerpolynom einfach vorhanden sind:
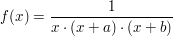
Ansatz für die Partialbruchzerlegung:
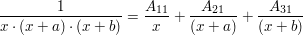
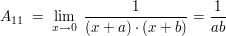 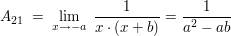 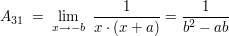
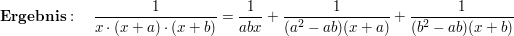
weitere Beispiele folgen :-)
|