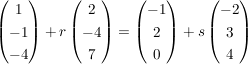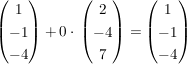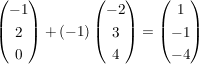GeradenschnittpunktGegeben sind zwei Geraden, gesucht ist ihr Schnittpunkt:
Zuerstmal: wenn man mehrere Variablen, und mehrere Gleichungen hat, dann nennt sich das ein "Lineares Gleichungssystem" (LGS).
Wir haben hier zwei Unbekannte und drei Gleichungen. Zum 'einfach nur lösen' würden uns zwei Gleichungen reichen, d.h. die dritte bleibt uns übrig, um damit die Probe zu machen (und in der Probe sehen wir dann, ob's auch wirklich einen Schnittpunkt gibt).
Ich schreib die drei Gleichungen nochmal auf:
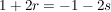 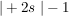
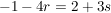 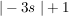
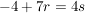 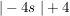
Jetzt ein wenig umformen - ich bringe alle Variablen auf eine Seite, und die konstanten Zahlen auf die andere Seite (also das, was ich hinter die Gleichungen geschrieben habe):
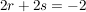
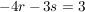
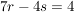
Um für r und s Lösungen zu finden, brauche ich nur zwei dieser drei Gleichungen. Dafür nehme ich einfach (willkürlich) die ersten beiden Gleichungen, und "spare" mir die dritte Gleichung für die Probe auf.
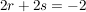
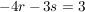
Um in der zweiten Gleichung das r wegzubekommen, multipliziere ich die erste Gleichung mit 2, und addiere die beiden Gleichungen.
Das kann man einfach im Kopf rechnen, was dann passiert, ich beschreib es mal kurz, bevor ich den nächsten Schritt hinschreibe:
Was passiert mit dem r? 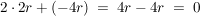 (genau das wollten wir ja). (genau das wollten wir ja).
Was passiert mit dem s? 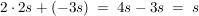
Was passiert mit den Zahlen? 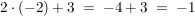
Somit bleibt nach der Aktion "2 mal erste Gleichung plus zweite Gleichung" das folgende LGS übrig (die erste Zeile bleibt unverändert, nur die zweite Zeile wird ersetzt):
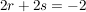
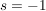
Aus der zweiten Gleichung kann man direkt 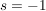 ablesen. ablesen.
Durch Einsetzen in die erste Gleichung erhält man: 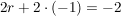  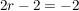  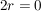 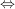 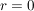 . .
Also hat die Rumrechnerei mit den ersten beiden Gleichungen folgenden Lösungen gebracht: 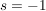 , und , und 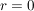 . .
Jetzt das wichtigste: die Probe in der dritten Gleichung 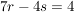 : :
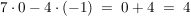 , also wahre Aussage, und somit schneiden sich die beiden Geraden in einem Punkt. , also wahre Aussage, und somit schneiden sich die beiden Geraden in einem Punkt.
Wenn du jetzt noch den Schnittpunkt brauchst, dann setzt du entweder das 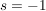 in die Geradengleichung ein, die das s enthält, oder eben das in die Geradengleichung ein, die das s enthält, oder eben das 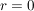 in die Geradengleichung, in der das r steht. Und (wieder) als Probe (ob du dich beim Einsetzen verrechnet hast) kannst du natürlich beides machen, es müsste sich beide Male derselbe Schnittpunkt ergeben (bzw. "Ortsvektor des Schnittpunktes", um's mathematisch korrekt auszudrücken). in die Geradengleichung, in der das r steht. Und (wieder) als Probe (ob du dich beim Einsetzen verrechnet hast) kannst du natürlich beides machen, es müsste sich beide Male derselbe Schnittpunkt ergeben (bzw. "Ortsvektor des Schnittpunktes", um's mathematisch korrekt auszudrücken).
Der Ortsvektor zum Schnittpunkt lautet also:
oder
|