HalbgruppeDefinition Halbgruppe
(enthalten: Definitionen für assoziative Halbgruppe, kommutative Halbgruppe, Halbgruppen-Homomorphismus, Unterhalbgruppe)
Schule
Universität
Es sei X eine nichtleere Menge. Eine innere Verknüpfung 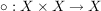 heißt assoziativ, wenn heißt assoziativ, wenn
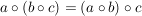
gilt für alle 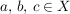 . .
Ein Paar 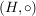 , bestehend aus einer nichtleeren Menge H und einer assoziativen inneren Verknüpfung , bestehend aus einer nichtleeren Menge H und einer assoziativen inneren Verknüpfung  auf H, heißt eine Halbgruppe. auf H, heißt eine Halbgruppe.
Bemerkung
Folgende (und andere) Redewendungen sind üblich:
H zusammen mit  ist eine Halbgruppe, oder H ist bezüglich ist eine Halbgruppe, oder H ist bezüglich  eine Halbgruppe, oder eine Halbgruppe, oder  definiert auf H eine Halbgruppenstruktur, wenn gilt: definiert auf H eine Halbgruppenstruktur, wenn gilt:
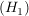 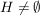 , ,
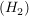 die Verknüpfung die Verknüpfung 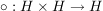 ist assoziativ. ist assoziativ.
Beispiele
(1) 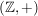 , , 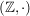 sind Halbgruppen. sind Halbgruppen.
(2) Für eine nichtleere Menge X sind 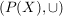 , , 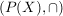 Halbgruppen. Halbgruppen.
(3) Ist 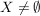 , dann ist , dann ist 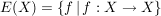 zusammen mit der Komposition von Abbildungen zusammen mit der Komposition von Abbildungen 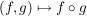 eine Halbgruppe. eine Halbgruppe.
Definition (abelsche Halbgruppe)
Eine Halbgruppe 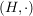 heißt kommutativ oder abelsch, wenn heißt kommutativ oder abelsch, wenn 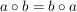 gilt für alle gilt für alle 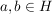 . .
Definition (Halbgruppen-Homomorphismus)
Sind 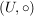 und und 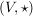 Halbgruppen, dann ist Halbgruppen, dann ist 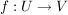 ein Halbgruppen-Homomorphismus, wenn ein Halbgruppen-Homomorphismus, wenn
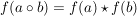
gilt für alle 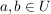 . .
Beispiel
Es ist für eine nichtleere Menge X
![$ f: \begin{array}{ccc} (P(X),\cap) & \to & (P(X),\cup) \\[5pt] A & \mapsto & f(A):=X \setminus A \end{array} $ $ f: \begin{array}{ccc} (P(X),\cap) & \to & (P(X),\cup) \\[5pt] A & \mapsto & f(A):=X \setminus A \end{array} $](/teximg/1/7/00392071.png)
ein Halbgruppen-Homomorphismus.
Definition (Unterhalbgruppe)
Eine nichtleere Teilmenge 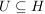 eine Halbgruppe eine Halbgruppe 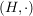 heißt Unterhalbgruppe (von H), wenn für alle heißt Unterhalbgruppe (von H), wenn für alle 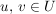 auch auch 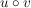 in U liegt. Die Restriktion von in U liegt. Die Restriktion von  auf auf 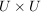 liefert dann eine innere Komposition auf U, diese ist assoziativ (denn liefert dann eine innere Komposition auf U, diese ist assoziativ (denn  ist bereits assoziativ auf H), d.h. ist bereits assoziativ auf H), d.h. 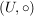 ist eine Halbgruppe. ist eine Halbgruppe.
Beispiele
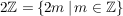 ist eine Unterhalbgruppe von ist eine Unterhalbgruppe von 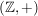 . .
Quelle: isbn3446130799
| 