Induktion2Wir sollen zeigen, dass 7 ein Teiler von 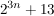 ist. ist.
Nun überprüfen wir, ob unsere Aussage für n=0 gilt:
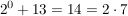
Wir sehen also, dass unsere Aussage für n=0 bewiesen ist.
Jetzt setzen wir voraus, dass wir unsere Aussage für n bewiesen haben.
Das heißt 7 ist ein Teiler von 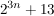 !! !!
Das ist unsere Induktionsvoraussetzung.
Nun überprüfen wir die Aussage für n+1.
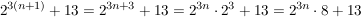
Bist du bei allen Rechenschritten mitgekommen? Wenn nicht, dann mach dich mit den Potenzgesetzen vertraut.
Wir rechnen weiter.
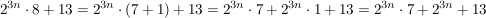
So, jetzt schauen wir uns mal unser Ergebnis an.
Wir stellen fest: 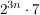 ist durch 7 teilbar. ist durch 7 teilbar.
Und: 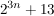 ist auch durch 7 teilbar, wenn du mir nicht glaubst, dann schau mal in unsere Voraussetzung ;-) ist auch durch 7 teilbar, wenn du mir nicht glaubst, dann schau mal in unsere Voraussetzung ;-)
Jetzt ist unser Beweis fertig. Wie das?
Wieso dürfen wir denn einfach voraussetzen, dass 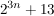 durch 7 teilbar ist? Und macht es überhaupt Sinn? durch 7 teilbar ist? Und macht es überhaupt Sinn?
Gibt es überhaupt ein solches n?
Fragen über Fragen ...
Also ein n gibt es auf jeden Fall, nämlich n=0. Das haben wir schon bewiesen. Und da wir gezeigt haben, dass - wenn die Ausage für n gilt, sie dann auch für n+1 gilt -, haben wir also auch schon die Aussage für 0+1 bewiesen.
Das heißt, wir haben noch ein n gefunden, für das unsere Ausage wahr ist, nämlich n=1. Und damit haben wir die Möglichkeit, uns von einer Zahl zur nächsten "durchzuhangeln", also: wenn die Aussage für n gilt,
dann gilt sie auch für n+1.
| 