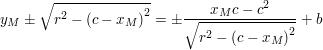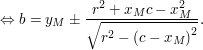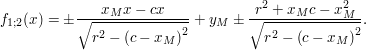KreisDefinition
Ein Kreis ist die Menge aller Punkte in einer Ebene, die von einem festen Punkt M (Mittelpunkt) die Entfernung r ("Radius") besitzen:
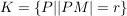 ( Umfang) oder 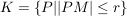 ( Kreisfläche)
Dies kann man auch mit Hilfe der Vektorrechnung beschreiben, wenn 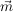 der Ortsvektor des Mittelpunkts M ist: der Ortsvektor des Mittelpunkts M ist:
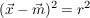
in Koordinaten ausgedrückt:
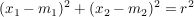
Umfang des Kreises
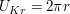
Flächeninhalte
Kreis
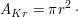
Kreissegment
Durch eine Sekante abgetrennter Teil eines Kreises
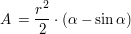
Siehe auch Wikipedia: Kreissegment
Kreissektor
Durch zwei Radien begrenzter Teil eines Kreises ("Kuchenstück")
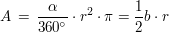
Siehe auch Wikipedia: Kreissektor
Berechnung von Kreistangenten
Aufgabe
Gegeben ist der Kreis K mit 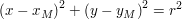 , der von der Geraden x = c mit , der von der Geraden x = c mit 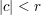 in den Punkten in den Punkten 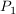 und und 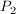 geschnitten wird. Man bestimme die Kreistangenten geschnitten wird. Man bestimme die Kreistangenten 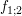 für für 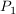 und und 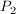 . .
Lösung
Wir gehen also von der allgemeinen Kreisgleichung eines Kreises K mit Mittelpunkt 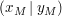 aus: aus: 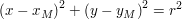 und formen diese nach y um, wodurch wir zwei Funktionen erhalten: und formen diese nach y um, wodurch wir zwei Funktionen erhalten:
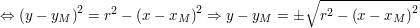
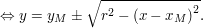
Angenommen eine senkrechte Gerade x=c schneidet K in den Punkten
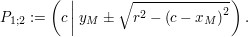
Bilden der Ableitungen
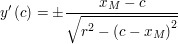
und Einsetzen von 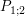 zusammen mit diesen Ableitungen in die allgemeine Geradengleichung f(x):=ax+b ergibt: zusammen mit diesen Ableitungen in die allgemeine Geradengleichung f(x):=ax+b ergibt:
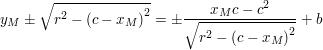
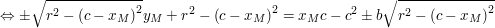
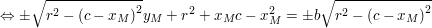
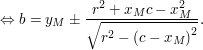
Allgemein erhalten wir also für die Kreistangenten in 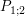 : :
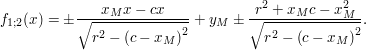
|