MaterialForum359Mechanik
Mechanik I
- Kräfte und Bewegungen
- Arbeit
- Energie
- Leistung
Kräfte und Bewegungen
Wirken auf einen Körper keinerlei Kräfte kommt es zu keiner Beschleunigung d.h. der Körper verbleibt entweder in seiner Ruhelage oder bewegt sich mit seiner momentanen Geschwindigkeit weiter (gleichförmige Bewegung mit konstanter Geschwindigkeit aufgrund des Trägheitsgesetzes).
Regel
Bei einer geradlinigen Bewegung eines Körpers mit konstanter Geschwindigkeit (also ohne Form von Beschleunigung) gilt für die Geschwindigkeit v:
Die Einheit der Geschwindigkeit ist:
Beispielaufgabe
Wie lange fliegt eine Brieftaube mit der Geschwindigkeit
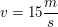 um eine Entfernung von um eine Entfernung von 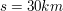 zu überwinden ? zu überwinden ?
Gesucht ist hier die Flugzeit t. Stellt man die Gleichung für die Geschwindigkeit nach t um, so kann man diese errechnen:
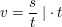
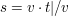
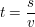
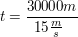
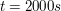
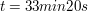
Die Flugzeit der Brieftaube beträgt also 33 Minuten und 20 Sekunden.
Wirkt auf einen Körper eine Kraft F, so ändert sich seine Bewegungsrichtung, seine Geschwindigkeit oder beides, er erfährt eine Beschleunigung. Bleibt diese Kraft F über einen Zeitraum konstant, ist auch die aus dieser Kraft resultierende Beschleunigung konstant (solange keine zusätzlichen Kräfte auftreten).
Regel
Bei einer geradlinigen Bewegung eines Körpers mit konstanter Beschleunigung gilt für die Geschwindigkeit v allgemein:
Wobei 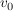 die Anfangsgeschwindigkeit zu Beginn des Beschleunigungsvorganges und a die Beschleunigung darstellt. t ist die Beschleunigungsdauer, also auch die Dauer der Krafteinwirkung die zur Beschleunigung des Körpers führt. die Anfangsgeschwindigkeit zu Beginn des Beschleunigungsvorganges und a die Beschleunigung darstellt. t ist die Beschleunigungsdauer, also auch die Dauer der Krafteinwirkung die zur Beschleunigung des Körpers führt.
Die Einheit der Beschleunigung ist:
Wird der Körper aus seiner Ruhelage heraus beschleunigt, so ist 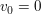 vereinfacht sich die Gleichung für die Geschwindigkeit zu: vereinfacht sich die Gleichung für die Geschwindigkeit zu:
Mithilfe dieser grundlegenden Gesetze lässt sich auch eine auf einen Körper wirkende Kraft berechnen.
Regel
Eine Kraft F lässt sich als Produkt aus der zu beschleunigenden Masse m und der wirkenden Beschleunigung beschreiben:
Wichtige in der Natur vorkommende Kräfte sind unter Anderem:
- Die magnetische Kraft, welche in der Umgebung eines Magneten entsteht. Magneten besitzen einen Nord- und einen Südpol, gleichnamige Pole stossen sich ab, unterschiedliche Pole ziehen sich an. Durch diese Kräfte entsteht entlang imaginärer Kraftlinien ein Magnetfeld, dessen Richtung immer vom Nordpol zum Südpol gerichtet ist und welches ausserhalb des Magneten liegt. Bestimmte, normalerweise nicht magnetische, Stoffe werden in der Nähe eines Magneten selbst zu Einem, man bezeichnet diese Eigenschaft als Ferromagnetismus.
- Die elektrische Kraft, welche zu Stande kommt, wenn sich Ladungsträger in einem elektrischen Leiter bewegen. Damit sie dies tun müssen sie beschleunigt werden, es muss also eine Krafteinwirkung statt finden. Im Fall der elektrischen Kraft sind es Abstossungskräfte zwischen gleichnamigen Ladungsträgern und Anziehungskräfte zwischen unterschiedlichen Ladungsträgern. Diese Kräfte sind umso grösser, je geringer die Abstände zwischen den Ladungsträgern sind. Ähnlich wie bei der magnetischen Kraft verläuft auch die elektrische Kraft entlang imaginärer Kraftlinien zwischen den Ladungen, die Kraftrichtung ist dabei festgelegt von positiven Ladungen zu negativen Ladungen. Sitzen auf einem Pol einer Spannungsquelle viele gleichnamige Ladungsträger sehr dicht beieinander, werden die Abstossungskräfte so gross, dass sich die Ladungsträger auf ungeladene Körper in der Umgebung verteilen oder zum entgegengesetzten Pol der Spannungsquelle fliessen.
- Gravitationskraft beruht auf den Anziehungskräften zwischen Körpern. Diese Anziehungskräfte sind direkt proportional zu den Massen der beteiligten Körper und umgekehrt proportional zum Abstand zwischen diesen.
- Reibungskraft entsteht bei der Berührung zweier Körper und der Bewegung dieser Körper aneinander vorbei.
physikalische Arbeit
Will man einen Körper beschleunigen, benötigt man eine auf ihn wirkende Kraft. Diese Kraft kennzeichnet sich durch einen Betrag (Stärke der Kraft), eine Richtung und sie besitzt am Körper einen Angriffspunkt.
Regel
Eine Kraft besitzt Vektorcharakter und ist gekennzeichnet durch Betrag und Richtung. Weiterhin besitzt sie am Körper auf den sie wirkt (mindestens) einen Angriffspunkt. Wirken auf einen Körper mehrere Kräfte kann man aus diesen eine resultierende Kraft (Ersatzkraft) bestimmen.
Will man einen Körper in Bewegung versetzen (beschleunigt man ihn also) verrichtet man an ihm physikalische Arbeit. Dabei ergibts sich diese als Produkt aus Kraft und Länge des Wegs. Verringert man nun zum Beispiel die Kraft, welche benötigt wird um einen Körper mit einer bestimmten Masse in Bewegung zu setzen (z.B. durch Kraftwandler beim Heben/Ziehen eines Körpers) muss man die Wegstrecke dementsprechend verlängern, womit die am Körper verrichtete physikalische Arbeit konstant bleibt.
Regel
Was man beim Verrichten einer physikalischen Arbeit an Kraft spart (z.B. durch Verwendung einer Maschine (Kraftwandler)) muss man an Wegstrecke zusetzen. Diese grundlegende Regel wird Goldene Regel der Mechanik genannt.
Die Grösse der physikalische Arbeit gibt also darüber Auskunft, wie stark eine auf einen Körper wirkende Kraft ist und über welche Wegstrecke diese Kraft gewirkt hat/wirkt.
Regel
Wirkt eine Kraft F auf einen Körper längs einer Wegstrecke s, so bezeichnet man das Produkt aus beiden Grössen als die physikalische Arbeit W:
Die Einheit der physikalischen Arbeit ist:
Hebt man einen Körper mit einer Masse m um eine Höhe h an, so verrichtet man an diesem Körper die Hubarbeit 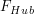 . Diese Arbeit bleibt im angehobenen Körper in Form von Energie gespeichert, die Energie des Körpers erhöht sich also (am Ausgangspunkt besass er nur eine Lageenergie). . Diese Arbeit bleibt im angehobenen Körper in Form von Energie gespeichert, die Energie des Körpers erhöht sich also (am Ausgangspunkt besass er nur eine Lageenergie).
Regel
Die Energie E, welche ein Körper besitzt, kennzeichnet die an ihm verrichtete physikalsische Arbeit W.
Die Einheit der Energie ist (analog zur physikalischen Arbeit):
Energie kann in verschiendensten Formen auftreten:
- potentielle Energie (Lageenergie):
Verrichtet man an einem Körper (in Ruhelage)Arbeit (z.B. durch Anheben) erhöht man seine potentielle Energie. Sie ist abhängig von der Masse des Körpers, der Erdbeschleunigung g und der Wegstrecke (bzw. der Hubhöhe):
- kinetische Energie (Bewegungsenergie):
Beschleunigt man einen Körper verrichtet man an ihm ebenfalls physikalische Arbeit, welche abhängig ist von der Grösse der angreifenden Kraft (also der Stärke der Beschleunigung) und der Wegstrecke über die der Körper beschleunigt wird (woraus man die Geschwindigkeit des Körpers ermitteln kann). Für die Berechung der kinetischen Energie gilt:
- Weitere bedeutende Formen von Energie, welche in anderen Kapiteln dieser Materialsammlung näher behandelt werden sind die elektrische Energie, die magnetische Energie und die Wärmeenergie.
Physikalische Energie und Arbeit sind also zwei eng in zusammenhang stehende Grössen. Erhöht man zum Beispiel die Lageenergie eines Körpers durch Hubarbeit, wo bleibt diese im Körper gespeichert. Verbindet man diesen Körper nun z.B. mit Hilfe von Seilzügen mit einem andern Objekt, so kann dieser Körper (z.B. durch Herunterfallen) durch Abgabe dieser in ihm gespeicherten Energie selbst Arbeit an diesem zweiten Körper verrichten (und diesen z.B. Anheben). Energie kann also niemals verloren gehen sondern nur ihre Form verändern.
Regel
Energie kann weder erzeugt noch vernichtet werden, sie ändert lediglich ihre Erscheinungsform. Diesen Leitsatz nennt man Energieerhaltungssatz und er tritt in verschiedenen Sonderformen in allen Teilgebieten der Physik auf.
Leistung
Eine weitere wichtige physikalische Grösse ist die der Leistung P. Sie ist abhängig von der Dauer des Vorgangs, bei dem eine physikalische Arbeit verrichtet wird. Als gutes Beispiel für eine unterschiedlich grosse Leistung betrachte man zwei Fahrzeuge: Beide haben die selbe Höchstgeschwindigkeit von 150 km/h und die selbe Masse (beide erhöhen beim Beschleunigen auf ihr Höchstgeschwindigkeit ihre kinetische Energie um den selben Betrag) brauchen jedoch unterschiedlich lange um diese zu erreichen. Somit bringt das Fahrzeug, welches schneller seine Höchstgeschwindigkeit erreicht eine höhere Leistung auf.
Regel
Je kürzer das Zeitintervall t, in dem eine physikalische Arbeit verrichtet wird, ist desto grösser ist die aufgebrachte Leistung:
Die Einheit der Leistung ist:
Thermodynamik
Thermodynamik I
- Temperaturänderung und Aggregatzustand
- Wärmeausdehnung von Gasen
- Wärneausdehnung von Festkörpern
Temperaturänderung und Aggregatzustand
Der Begriff Wärme umschreibt im physikalischen Sinne eine weitere Form von Energie. Um die Auswirkungen und Zusammenhänge der Wärmeenergie auf Festkörper, Flüssigkeiten und Gase zu verstehen muss man sich grundlegend mit der Teilchenstruktur der Materie befassen.
Materie setzt sich aus winzig kleinen Bausteinen, den
Atomen zusammen. Durch Variationen im Aufbau dieser Materie treten die drei Aggregatzustände fest, flüssig und gasförmig auf, wobei die meisten chemischen Elemente unter bestimmten Bedingungen sowohl im festen, gasförmigen als auch im flüssigen Zustand auftreten können.
Führt man einem Stoff nun Wärmeenergie zu, so erhöht sich die Temperatur des Körpers, Energie und Temperatur sind also zwei grundlegende Grössen der Thermodynamik.
Regel
Führt man einem Stoff eine bestimmte Menge an Wärmeenergie zu, so erhöht sich seine Temperatur. Die Energiemenge die nötig ist um ein Kilogramm eines Stoffes um ein Kelvin zu erwärmen ist definiert als die spezifische Wärmekapität c dieses Stoffes. Für die Berechnung der Energiemenge die zur Erwärmung einer gegebenen Stoffmenge nötig ist gilt:
Die Temperaturerhöhung lässt sich mit Hilfe der atomaren Struktur der Stoffe erklären. In einem Feststoff sind die Atome nachbarschaftlich verbunden, haben so relativ wenig Bewegungsfreiheit. Sie schwingen jedoch um ihre Mittellage und wandeln so stetig Spannenergie in kinetische Energie um. Je stärker die Atome schwingen, desto höher ist die Temperatur eines Festkörpers. Führt man einem Festkörper sehr viel Energie zu, so werden die Schwingungen extrem stark und die zwischenatormaren Verbindungen können annähernd zerstört werden. Geschieht dies, geht eine feste Substanz in den flüssigen Aggregatzustand über, man nennt dies Schmelzen.
Im flüssigen Zustand sind die Teilchen weniger stark aneinander gebunden, sie können sich relativ frei in einem Raum bewegen. Führt man nun Energie zu nehmen die Bewegungen der Atome weiter zu und die Temperatur der Flüssigkeit erhöht sich. Sind die Bewegungen der Atome aufgrund des hohen Energiegehalts des Systems sehr stark, gehen auch die letzten zwischenatomaren Bindungen verloren, die Atome können sich völlig frei bewegen, die Flüssigkeit wechselt in den gasförmigen Aggregatzustand. Mann nennt dies Sieden oder Verdampfen. Siedet/verdampft eine Flüssigkeit, liegt ihre Temperatur stehts weit oberhalt der Mindestsiedetemperatur, alle Atome der Flüssigkeit haben dann genügend Energie (bewegen sich stark genug). Die Temperatur eines Körpers zeigt allerdings nur die durchschnittliche Bewegungsenergie aller Teilchen an, einige der Teilchen erhalten früher oder später als andere genügend Energie um die atomaren Strukturen zu verlassen. Man bezeichnet dies als Verdunsten (zu beobachten beim Kochen von Wasser).
Man kann also erkennen, dass sich, wenn man die Temperatur eines Stoffes erhöht sich auch die (mittlere) kinetische Energie der Teilchen dieses Stoffes erhöht. Man bezeichnet diesen Vorgang als Erhöhung der inneren Energie eines Systems. Analog dazu gilt dies für die Verringerung der inneren Energie eines Systems und Energieabgabe.
Regel
Die innere Energie eines Systems lässt sich durch Zufuhr oder Abgabe von Energie ändern, Energie darf nicht verloren gehen sondern darf nur ihre Erscheinungsform ändern. Die Gesamtenergie muss dabei unverändert bleiben. Man bezeichnet dies als 1. Hauptsatz der Thermodynamik, er stellt eine Sonderform des Energieerhaltungssatzes dar.
Wie man erkennen kann, finden die Übergänge zwischen den Aggregatzuständen fliessend und unter bestimmten Bedingungen statt.
Regel
Materie kann in den Aggregatzuständen fest, flüssig und gasförmig annehmen (Sonderfälle unter extremen Bedingungen sind Plasma und Bose-Einstein-Kondensat). Übergänge zwischen den einzelnen Aggregatzuständen finden bei materialspezifischcen Schmelz- und Siedetemperaturen statt.
Die zum Schmelzen/Verdampfen nötige Energie nennt man Schmelz-/
Verdampfungswärme(-energie). Diese Grössen sind materialspezifische Konstanten, also stoffabhängig.
Um den Zusammenhang zwischen Temperatur eines Körpers und der inneren Energie dieses Systems deutlich erkennen zu können, verwendet man zur Angabe einer Temperatur anstatt der Celciusskala (welche als Standart für den Alltagsgebrauch gilt) die Kelvinskala und bezeichnet Werte, welche in dieser Einheit angegeben werden als absolute Temperatur. Für diese gilt eine direkte Proportionalität zur inneren Energie, man kennzeichnet die Temperatur (auf der Celciusskala) formal mit dem griechischen Buchstaben Theta, die absolute Temperatur (auf der Kelvinskala) mit dem deutschen Buchstaben T. Für die Umrechnung zwischen Celcius- und Kelvinskala gilt:
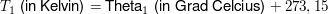
Durch die direkte Proportionalität zwischen innerer Energie und absoluter Temperatur lässt sich ein absoluter Nullpunkt bestimmen, an jegliche Teilchenbewegung zum absoluten Stillstand kommt wobei somit auch die innere Energie des Systems nahezu Null beträgt. Die absolute Temperaturnullpunkt ist der Ursprung der Kelvinskala (also 0 Kelvin, auf der Celciusskala entspricht dies -273,15 Grad Celcius) und man kann ihn nicht unterschreiten oder aus einem System entfernen.
| 