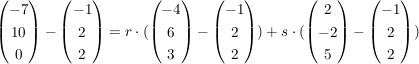PunktprobeWann liegt ein Punkt D auf einer durch A, B, C gegebenen Ebene?
Gegeben seien A (-1|2|2) mit dem Ortsvektor 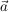 , B (-4|6|3), C (2|-2|5). , B (-4|6|3), C (2|-2|5).
Diese drei Punkte bilden also eine Ebene:
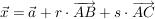
Wenn nun ein Punkt D auf dieser Ebene liegen soll, müssen seine Koordinaten die Ebenengleichung erfüllen,
das bedeutet, es muss zwei reelle Zahlen r, s geben, so dass gilt:
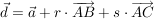
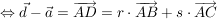
die letzte Gleichung kann man auch so beschreiben: der Vektor 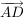 muss sich aus den beiden anderen Vektoren linear kombinieren lassen oder durch eine Linearkombination beschreiben lassen. muss sich aus den beiden anderen Vektoren linear kombinieren lassen oder durch eine Linearkombination beschreiben lassen.
Konkret mit D(-7|10|0):
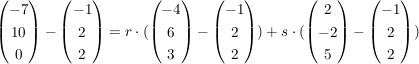
Die Komponenten fasst man zusammen und schreibt das Ganze als lineares Gleichungssystem auf:
-6 = r * (-3) + s*3
8 = r * 4 + s *(-4)
-2 = r *1 + s*3
Dieses LGS läßt sich lösen mit r=1 und s=-1  der Punkt D liegt auf der durch A,B,C bestimmten Ebene. der Punkt D liegt auf der durch A,B,C bestimmten Ebene.
Hätte man statt dessen den Punkt (7|10|0) geprüft:

8 = r * (-3) + s*3
8 = r * 4 + s *(-4)
-2 = r *1 + s*3
aus den unteren beiden Gleichungen hätte sich wieder r=1 und s=-1 ergeben, weil sich dort ja nichts verändert hat.
Aber die "Probe" mit der ersten Gleichung
8 = -3 -3 wäre nicht aufgegangen  dieser Punkt läge nicht auf der Ebene. dieser Punkt läge nicht auf der Ebene.
|