TeleskopsummeIst 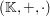 ein Körper und ist ein Körper und ist 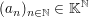 eine Folge in eine Folge in 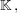 so bezeichnen wir für so bezeichnen wir für 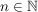 eine Summe der Form eine Summe der Form
als Teleskopsumme.
Für eine solche gilt
Beispiel:
 Besonders nützlich ist die Teleskopsumme bei der Berechnung des Reihenwertes von Besonders nützlich ist die Teleskopsumme bei der Berechnung des Reihenwertes von 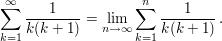 Für jedes Für jedes 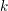 gilt nämlich offenbar gilt nämlich offenbar
so dass sich mit 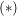 folgendes ergibt folgendes ergibt
Bemerkung:
Offenbar gibt es folgenden trivialen Zusammenhang zwischen einem endlichen Produkt und der Teleskopsumme:
Sind alle 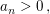 so folgt so folgt
Dabei wurde die Regel 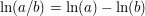 für für 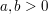 angewendet; die interessante Beziehung dabei ist blaumarkiert, und sie ist interessant in der Anwendung, wenn man sie von rechts nach links benutzt. angewendet; die interessante Beziehung dabei ist blaumarkiert, und sie ist interessant in der Anwendung, wenn man sie von rechts nach links benutzt.
Beispiel zur Bemerkung:
Man betrachte 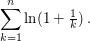 Hier gilt Hier gilt
Arbeitet man lieber mit Produkten, so kann man unter Verwendung des blaumarkierten Teils auch rechnen
Hier wurde die Beziehung 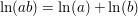 für für 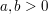 verwendet. verwendet.
Teleskopsummen verwendet man insbesondere, um Aussagen über Teleskopreihen erzielen zu können! Ferner nennt man eine Teleskopsumme auch Ziehharmonikasumme.
(Zudem: Siehe auch Teleskopverknüpfung.)
| 