UmkehrfunktionVersion 4 von Fr 08.10.2004 um 15:59(Unterschied) ← Nächstältere Version | Aktuelle Version ansehen| Nächstjüngere Version → (Unterschied) Definition Umkehrfunktion
Seien D und Z nichtleere Mengen.
Ist eine Funktion 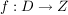 bijektiv, so existiert eine Funktion bijektiv, so existiert eine Funktion 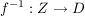 mit folgenden zwei Eigenschaften: mit folgenden zwei Eigenschaften:
1.) 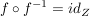
2.) 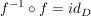
In diesem Fall heißt 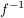 die Umkehrfunktion von f. die Umkehrfunktion von f.
Die Funktion 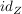 (bzw. (bzw. 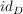 ) ist dabei die Identität auf Z (bzw. D). ) ist dabei die Identität auf Z (bzw. D).
Beispiele.
TODO
Bemerkungen.
1.) Die Umkehrfunktion 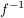 einer bijektiven Funktion einer bijektiven Funktion 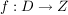 ordnet jedem Element aus dem Zielbereich Z genau ein Element des Definitionsbereiches zu. ordnet jedem Element aus dem Zielbereich Z genau ein Element des Definitionsbereiches zu.
2.) Ist 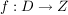 bijektiv, so ist auch die Umkehrfunktion bijektiv, so ist auch die Umkehrfunktion 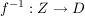 eine bijektive Funktion. eine bijektive Funktion.
| 