WurzelDefinition: Die n-te Wurzel aus einer reellen, nicht negativen Zahl  ist diejenige nicht negative Zahl ist diejenige nicht negative Zahl  mit mit 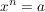
Wurzeln als Potenzen: Wurzeln können statt mit dem Wurzelsymbol auch als Potenzen geschrieben werden:
- Das Rechnen mit Wurzeln ergibt sich deshalb aus den Potenzgesetzen.
Spezialfälle:
- Quadratwurzel
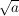 (ohne Wurzelindex geschrieben) steht für (ohne Wurzelindex geschrieben) steht für ![$ \wurzel[2]{a}=a^\bruch{1}{2} $ $ \wurzel[2]{a}=a^\bruch{1}{2} $](/teximg/3/0/00984103.png)
- Kubikwurzel
![$ \wurzel[3]{a}=a^\bruch{1}{3} $ $ \wurzel[3]{a}=a^\bruch{1}{3} $](/teximg/3/5/00984153.png)
Wurzeln aus negativen Zahlen?
Die "offizielle" Betrachtungsweise ist, dass grundsätzlich alle Wurzeln (auch solche mit ungeraden Wurzelexponenten) und Potenzen mit gebrochenen Exponenten nur für nichtnegative Zahlen, also für 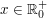 definiert sind und stets einen eindeutigen Wert in definiert sind und stets einen eindeutigen Wert in 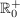 haben. Danach ist etwa haben. Danach ist etwa ![$ \wurzel[3]{-8} $ $ \wurzel[3]{-8} $](/teximg/3/9/00205793.png) oder eine Potenz wie oder eine Potenz wie 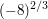 einfach gar nicht definiert. einfach gar nicht definiert.
Betrachtet man dann zum Beispiel die Gleichung 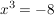 , so hat diese natürlich sehr wohl die Lösung , so hat diese natürlich sehr wohl die Lösung 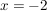 , aber man darf diese nicht schreiben als , aber man darf diese nicht schreiben als
![$ x = \wurzel[3]{-8} $ $ x = \wurzel[3]{-8} $](/teximg/2/7/00984072.png)
und auch nicht als
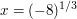
sondern als
![$ x = - \wurzel[3]{|-8|} = - |-8|^{1/3} $ $ x = - \wurzel[3]{|-8|} = - |-8|^{1/3} $](/teximg/9/9/00984099.png)
Man mag das als komplizierter als nötig betrachten, aber mit dieser konsequenten und einheitlichen Behandlung aller Wurzelausdrücke erspart man sich viele andere Komplikationen.
In heutigen Taschenrechnern wird leider keine einheitliche Definition befolgt. Bei gewissen Rechnern werden Kubikwurzeln aus negativen Zahlen akzeptiert und bei anderen gibt es (wie es sein sollte) eine Fehlermeldung.
Siehe zu dem Thema auch: Wurzeln aus negativen Zahlen
sowie: Diskussion
Wurzeln im Komplexen
Im Bereich 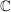 der komplexen Zahlen ist die Verwendung von Wurzelausdrücken noch problematischer als etwa die Benützung von Kubikwurzeln aus negativen Zahlen. Schon die Schreibweise der komplexen Zahlen ist die Verwendung von Wurzelausdrücken noch problematischer als etwa die Benützung von Kubikwurzeln aus negativen Zahlen. Schon die Schreibweise 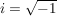 für die komplexe Einheit ist nicht unbedingt glücklich, da die Gleichung für die komplexe Einheit ist nicht unbedingt glücklich, da die Gleichung 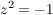 in in 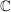 zwei Lösungen hat, nämlich zwei Lösungen hat, nämlich 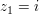 und und 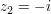 . .
Für die komplexen Lösungen der Gleichung 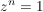 findet man zwar oft den Begriff "Einheitswurzeln", allerdings hat man es dann nicht mehr mit einer eindeutigen Wurzelfunktion zu tun, sondern mit den verschiedenen Elementen einer Lösungsmenge. findet man zwar oft den Begriff "Einheitswurzeln", allerdings hat man es dann nicht mehr mit einer eindeutigen Wurzelfunktion zu tun, sondern mit den verschiedenen Elementen einer Lösungsmenge.
| 