UmkehrfunktionVersion 14 von Sa 20.11.2004 um 23:40(Unterschied) ← Nächstältere Version | Aktuelle Version ansehen| Nächstjüngere Version → (Unterschied) Definition Umkehrfunktion
Seien 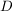 und und 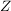 nichtleere Mengen. nichtleere Mengen.
Ist eine Funktion 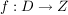 bijektiv, so existiert eine Funktion bijektiv, so existiert eine Funktion 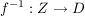 mit folgenden zwei Eigenschaften: mit folgenden zwei Eigenschaften:
1.) 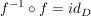
2.) 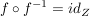
In diesem Fall heißt 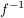 die Umkehrfunktion von die Umkehrfunktion von 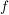 . .
Die Funktion 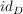 (bzw. (bzw. 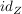 ) ist dabei die Identität auf ) ist dabei die Identität auf 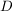 (bzw. (bzw. 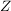 ). ).
Beispiele.
1.) Die Funktion 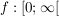 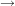 ![$ ]-\infty;-3] $ $ ]-\infty;-3] $](/teximg/6/1/00387816.png) definiert durch definiert durch 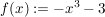 ist bijektiv. ist bijektiv.
Wir berechnen die zugehörige Umkehrfunktion:
Dazu geben wir uns ein festes 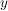 aus dem Zielbereich der Funktion aus dem Zielbereich der Funktion 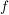 vor und suchen ein vor und suchen ein  aus dem Definitionsbereich mit aus dem Definitionsbereich mit 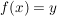 . Wir haben also die Gleichung . Wir haben also die Gleichung 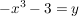 nach nach  aufzulösen: aufzulösen:
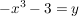
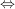
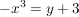
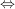
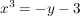
![$ x=\wurzel[3]{-y-3} $ $ x=\wurzel[3]{-y-3} $](/teximg/1/2/00387821.png)
Die Umkehrfunktion zu obiger Funktion 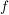 ist also gegeben durch die Vorschrift: ist also gegeben durch die Vorschrift:
![$ f^{-1}(y)=\wurzel[3]{-y-3} $ $ f^{-1}(y)=\wurzel[3]{-y-3} $](/teximg/2/2/00387822.png) . .
Da man Funktionen meißt in Abhängigkeit vom Parameter  schreibt, schreiben wir anstelle des Parameters schreibt, schreiben wir anstelle des Parameters 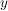 den Parameter den Parameter  : :
![$ f^{-1}(x)=\wurzel[3]{-x-3} $ $ f^{-1}(x)=\wurzel[3]{-x-3} $](/teximg/3/2/00387823.png)
Somit gelangen wir zum Ergebnis:
Die Umkehrfunktion zu der (bijektiven) Funktion 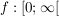 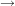 ![$ ]-\infty;-3] $ $ ]-\infty;-3] $](/teximg/6/1/00387816.png) definiert durch definiert durch 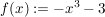 ist gegeben durch: ist gegeben durch:
![$ f^{-1}: ]-\infty;-3] $ $ f^{-1}: ]-\infty;-3] $](/teximg/4/2/00387824.png) 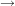 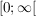 und der Rechenvorschrift und der Rechenvorschrift ![$ f^{-1}(x)=\wurzel[3]{-x-3} $ $ f^{-1}(x)=\wurzel[3]{-x-3} $](/teximg/3/2/00387823.png) . .
Bemerkungen.
1.) Die Umkehrfunktion 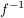 einer bijektiven Funktion einer bijektiven Funktion 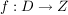 ordnet jedem Element aus dem Zielbereich ordnet jedem Element aus dem Zielbereich 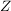 genau ein Element des Definitionsbereiches zu. genau ein Element des Definitionsbereiches zu.
2.) Ist 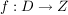 bijektiv, so ist auch die Umkehrfunktion bijektiv, so ist auch die Umkehrfunktion 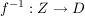 eine bijektive Funktion. eine bijektive Funktion.
3.) Man beachte, dass man 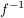 lediglich als Symbol für die Umkehrfunktion einer Funktion lediglich als Symbol für die Umkehrfunktion einer Funktion 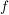 (im Falle der Existenz der Umkehrfunktion; also wenn (im Falle der Existenz der Umkehrfunktion; also wenn 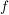 bijektiv ist) benutzt. Die Gefahr der Verwechslung mit dem Ausdruck bijektiv ist) benutzt. Die Gefahr der Verwechslung mit dem Ausdruck 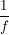 wird meist ausgeschlossen, weil sich meist aus dem Zusammenhang ergibt, ob wird meist ausgeschlossen, weil sich meist aus dem Zusammenhang ergibt, ob 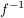 als Symbol für die Umkehrfunktion (einer Funktion als Symbol für die Umkehrfunktion (einer Funktion 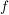 ) benutzt wird oder nicht. ) benutzt wird oder nicht.
| 