Funktionenscharuntersuchung
Schule
Gegeben sei die Funktionenschar durch
Dabei sei 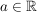 eine beliebige, aber feste Zahl; für jedes a ergibt sich dadurch eine weitere Funktion, die mit den anderen jedoch bestimmt Eigenschaften gemeinsam hat. eine beliebige, aber feste Zahl; für jedes a ergibt sich dadurch eine weitere Funktion, die mit den anderen jedoch bestimmt Eigenschaften gemeinsam hat.
Als erstes untersucht man die Funktion wie bei einer "normalen" Funktionsuntersuchung2 auf Schnittpunkte mit den Achsen, Extrem- und Wendestellen, usw.
Dabei muss man nur beachten, dass a eine reelle Konstante ist!
Anschließend kann man feststellen, dass
- sich alle Funktionen in einem bestimmten Punkt schneiden,
- an einer bestimmten Stelle dieselbe Steigung haben,
- oder weitere Eigenschaften, die sich aus den speziellen Eigenschaften der Schar ergeben.
- Man kann danach auch fragen, auf welchen (Funktions-)Kurven sich die Extrem- oder Wendepunkte bewegen, wenn man für den Parameter unterschiedliche Werte einsetzt (siehe Ortskurven).
1. Alle Funktionen schneiden sich in einem Punkt:
Man wählt zwei verschiedene Parameterwerte a und b mit 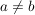
und untersucht, an welchen Stellen die Funktionswerte übereinstimmen:
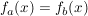
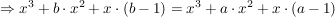
nach x auflösen ergibt: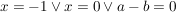
Da 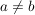 vorausgesetzt ist, kommt die dritte "Lösung" nicht in Frage, wohl aber die beiden anderen: alle Funktionen dieser Schar schneiden sich an den Stellen -1 und 0, d.h. in den Punkten vorausgesetzt ist, kommt die dritte "Lösung" nicht in Frage, wohl aber die beiden anderen: alle Funktionen dieser Schar schneiden sich an den Stellen -1 und 0, d.h. in den Punkten 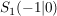 mit der Steigung mit der Steigung 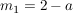 und und 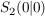 mit mit 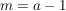 . .
2. Alle Funktionen haben an derselben Stelle dieselbe Steigung:
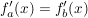
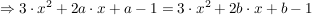
nach x auflösen ergibt: 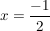
Für alle Funktionen ergibt sich bei 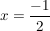 dieselbe Steigung: dieselbe Steigung:
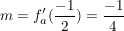 , ganz unabhängig von a. , ganz unabhängig von a.
| 