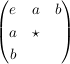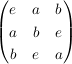GruppeDefinition Gruppe
Eine Menge  zusammen mit einer Verknüpfung " zusammen mit einer Verknüpfung " " heißt Gruppe " heißt Gruppe 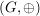 , wenn gilt: , wenn gilt:
G1) Für alle 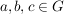 ist ist 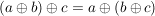 ("Assoziativität") ("Assoziativität")
G2) Es existiert ein 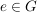 , so dass für alle , so dass für alle 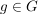 gilt: gilt: 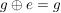 bzw. bzw. 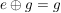 . ("Neutrales Element") . ("Neutrales Element")
(Statt  schreibt man bei additiver Schreibweise der Gruppe kurz: schreibt man bei additiver Schreibweise der Gruppe kurz: 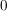 .) .)
G3) Für alle 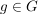 existiert ein existiert ein 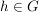 , so dass , so dass 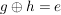 bzw. bzw. 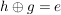 . ("Inverses Element") . ("Inverses Element")
(Statt 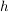 schreibt man bei additiver Schreibweise der Gruppe kurz: schreibt man bei additiver Schreibweise der Gruppe kurz: 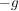 .) .)
Eine Gruppe heißt abelsch oder kommutative Gruppe, wenn zusätzlich das Kommutativgesetz gilt:
G4) Für alle 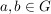 ist ist 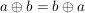 . .
Dabei sei angemerkt: Es ist 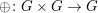 und man schreibt und man schreibt 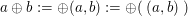 für für 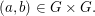
Bemerkungen:
(1) Ohne die in der Anmerkung erwähnte Notation würde man etwa das Assoziativitätsgesetz schreiben als
mihilfe der Konvention 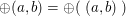 auch etwas knapper als auch etwas knapper als
Alleine dieses Beispiel zeigt schon deutlich den Vorteil der oben erwähnten Schreibweise!
(2) In einer Gruppe gilt das Assoziativgesetz auch für je endlich viele Elemente. Man nennt dies auch das verallgemeinerte Assoziativgesetz.
In multiplikativer Schreibweise lauten diese vier Bedingungen:
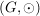 Gruppe, wenn: Gruppe, wenn:
G1) Für alle 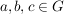 ist ist 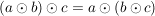 ("Assoziativität") ("Assoziativität")
G2) Es existiert ein 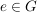 , so dass für alle , so dass für alle 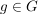 gilt: gilt: 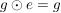 bzw. bzw. 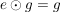 . ("Neutrales Element") . ("Neutrales Element")
(Statt  schreibt man bei multiplikativer Schreibweise der Gruppe kurz: schreibt man bei multiplikativer Schreibweise der Gruppe kurz: 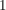 .) .)
G3) Für alle 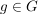 existiert ein existiert ein 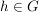 , so dass , so dass 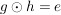 bzw. bzw. 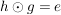 . ("Inverses Element") . ("Inverses Element")
Statt 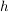 schreibt man bei multiplikativer Schreibweise der Gruppe kurz: schreibt man bei multiplikativer Schreibweise der Gruppe kurz: 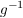
kommutative Gruppe: G4) Für alle 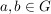 ist ist 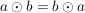 . .
Definition aus dem Meyberg
Ein Paar 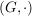 heißt eine Gruppe, wenn gilt: heißt eine Gruppe, wenn gilt:
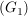 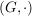 ist eine Halbgruppe, ist eine Halbgruppe,
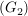 in in 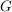 gibt es ein linksneutrales Element gibt es ein linksneutrales Element  , ,
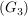 zu jedem zu jedem 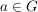 gibt es ein gibt es ein 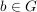 mit mit 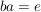 . (Existenz linksinverser Elemente) . (Existenz linksinverser Elemente)
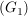 beinhaltet, dass beinhaltet, dass 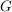 eine nichtleere Menge ist mit assoziativer Multiplikation. eine nichtleere Menge ist mit assoziativer Multiplikation.
Eine Gruppe 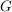 heißt abelsch oder kommutativ, wenn heißt abelsch oder kommutativ, wenn 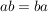 gilt für alle gilt für alle 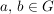 . .
Bemerkungen
1) Mit diesem ("schwachen") Axiomensystem kann man sehr schnell entscheiden, ob eine gegebene Halbgruppe eine Gruppe ist oder nicht.
2) Die endlichen Permutationsgruppen bilden den Ursprung einer allgemeinen Gruppentheorie. E. Galois (1811-1832) erkannte als erster die Bedeutung der Permutationsgruppen für die Bedeutung der Permuationsgruppen für die Theorie algebraischer Gleichungen und hat damit wesentlich das Interesse an diesen Gruppen belebt. Der heute vorliegende (abstrakte) Gruppenbegriff geht auf A. Cayley (1821-1895) zurück. Bis in neuerer Zeit wurden ständig neue Anwendungsmöglichkeiten der Gruppentheorie in Geometrie, Analysis, Topologie entdeckt. Gruppen spielen auch eine wichtige Rolle in der Kristallographie, Quantenmechanik und anderen theoretischen Naturwissenschaften.
Beispiele.
a) 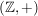 , , 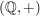 , , 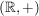 , , 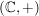 sind (additive) abelsche Gruppen. sind (additive) abelsche Gruppen.
b) 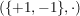 , , 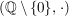 , , 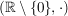 , , 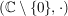 sind (multiplikative) abelsche Gruppen. sind (multiplikative) abelsche Gruppen.
c) 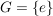 mit mit 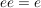 ist eine Gruppe. ist eine Gruppe.
d) Für jede natürliche Zahl  ist ist 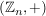 , die Menge der Restklassen modulo , die Menge der Restklassen modulo  , eine abelsche Gruppe der Ordnung , eine abelsche Gruppe der Ordnung  . Es ist . Es ist
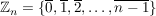
und 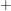 ist erklärt durch ist erklärt durch
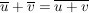 . .
Das neutrale Element ist 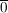 und und 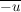 ist das Inverse (bwz. Addition) von ist das Inverse (bwz. Addition) von 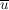 . Man berechnet . Man berechnet 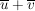 , indem man von , indem man von 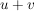 den bei Division durch den bei Division durch  enstehenden Rest enstehenden Rest  ermittelt; dann ist ermittelt; dann ist
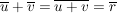 . .
(Man will doch der Summe ansehen, welches der Elemente aus 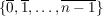 sie darstellt.) sie darstellt.)
Man beachte ferner, dass aus der Definition mit leichter Induktion
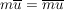 für alle für alle 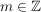
folgt.
e) Es sei
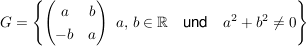 . .
Als Produkt wird das Matrizenprodukt genommen; dann ist 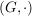 eine abelsche Gruppe. eine abelsche Gruppe.
f) Eine große Klasse von Beispielen erhält man aus folgendem Ergebnis:
Ist 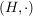 eine Halbgruppe mit neutralem Element und eine Halbgruppe mit neutralem Element und 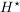 die Menge der invertierbaren Elemente aus die Menge der invertierbaren Elemente aus 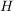 , dann ist , dann ist 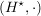 eine Gruppe. eine Gruppe.
Als triviale Anwendungen hiervon erhalten wir die Beispiele in b) aus den Halbgruppen 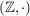 , , 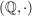 , , 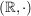 und und 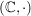 . Weitere Anwendungen werden in g), h) und i) angegeben. . Weitere Anwendungen werden in g), h) und i) angegeben.
g) Für 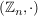 ist ist
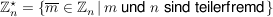 . .
Die Gruppe 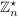 heißt prime Restklassengruppe modulo heißt prime Restklassengruppe modulo  . Die Ordnung . Die Ordnung 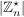 wird mit wird mit 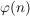 bezeichnet. bezeichnet. 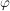 heißt die Eulersche heißt die Eulersche 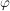 -Funktion. Es ist -Funktion. Es ist 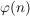 gleich der Anzahl der zu gleich der Anzahl der zu  teilerfremden ganzen Zahlen teilerfremden ganzen Zahlen 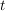 mit mit 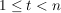 . .
h) Die Menge 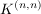 aller aller 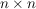 -Matrizen über einem Körper -Matrizen über einem Körper 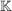 ist zusammen mit der Matrizenmultiplikation eine Halbgruppe mit der Einheitsmatrix als neutralem Element. Die invertierbaren Elemente in dieser Halbgruppe sind genau die Matrizen mit von Null verschiedener Determinante, d.h. ist zusammen mit der Matrizenmultiplikation eine Halbgruppe mit der Einheitsmatrix als neutralem Element. Die invertierbaren Elemente in dieser Halbgruppe sind genau die Matrizen mit von Null verschiedener Determinante, d.h.
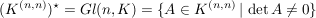 . .
i) symmetrische Gruppe
j) Es sind vielfach gewisse Teilmengen der symmetrischen Gruppe 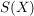 von von 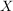 , die besonders ausgezeichnet sind. Ist auf , die besonders ausgezeichnet sind. Ist auf 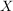 eine algebraische Struktur erklärt, so betrachtet man die Homomorphismen aus eine algebraische Struktur erklärt, so betrachtet man die Homomorphismen aus 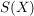 , die Automorphismen. Ist , die Automorphismen. Ist 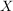 ein topologischer Raum, dann sind die topologischen Abbildungen von ein topologischer Raum, dann sind die topologischen Abbildungen von 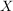 ( (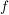 und und 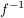 stetig) von besonderem Interesse. Betreibt man in stetig) von besonderem Interesse. Betreibt man in 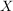 Geometrie, dann sind es die Translationen, Rotationen, Spiegelungen oder allgemeiner die projektiven bzw. affinen Abbildungen aus Geometrie, dann sind es die Translationen, Rotationen, Spiegelungen oder allgemeiner die projektiven bzw. affinen Abbildungen aus 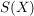 , die studiert werden. In allen diesen erwähnten Fällen zeigt man, dass die betrachtete Teilmenge von , die studiert werden. In allen diesen erwähnten Fällen zeigt man, dass die betrachtete Teilmenge von 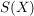 zusammen mit der gegebenen Multiplikation aus zusammen mit der gegebenen Multiplikation aus 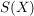 Gruppen sind. Die Struktur solcher Gruppen gibt Einblick in die jeweilige Struktur auf Gruppen sind. Die Struktur solcher Gruppen gibt Einblick in die jeweilige Struktur auf 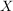 (und umgekehrt, natürlich). (und umgekehrt, natürlich).
k) Endliche Gruppen (mit nicht zu hoher Ordnung) übersieht man am besten, wenn sämtliche Produkte aufgeführt sind, wenn also die Verknüpfungstafel angegeben ist. In der Verknüpfungstafel einer Gruppe 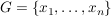 , Gruppentafel von , Gruppentafel von 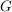 genannt, wählen wir stets genannt, wählen wir stets 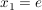 und können damit auf die Ränder verzichten, denn in der ersten Zeile stehen dann die Elemente und können damit auf die Ränder verzichten, denn in der ersten Zeile stehen dann die Elemente 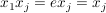 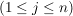 und in der ersten Spalte stehen und in der ersten Spalte stehen 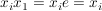 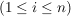 . .
Die Verknüfungstafel einer endlichen Halbgruppe ist genau dann eine Gruppentafel, wenn in jeder Zeile und jeder Spalte der Tafel jedes Element von  höchstens einmal vorkommt. höchstens einmal vorkommt.
Wenn wir aus gegebenen Informationen einige Plätze in der Gruppentafel auffüllen können, wissen wir, dass diese Elemente nicht noch einmal in derselben Zeile oder Spalte vorkommen können. Damit sind die Möglichkeiten zum Auffüllen der freien Plätze eingeschränkt.
l) Zur Illustration von k): Es sei 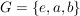 eine Gruppe mit neutralem Element eine Gruppe mit neutralem Element  . Von der Gruppentafel kann man die erste Zeile und erste Spalte sofort hinschreiben: . Von der Gruppentafel kann man die erste Zeile und erste Spalte sofort hinschreiben:
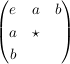
An die mit  gekennzeichnet Stelle muss gekennzeichnet Stelle muss 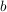 gesetzt werden; denn setzen wir dorthin gesetzt werden; denn setzen wir dorthin  , dann muss darunter , dann muss darunter 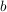 eingetragen werden und wir erhalten zweimal eingetragen werden und wir erhalten zweimal 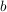 in der letzten Zeile. Nun liegen aber nach k) die anderen Stellen ebenfalls fest. Auf in der letzten Zeile. Nun liegen aber nach k) die anderen Stellen ebenfalls fest. Auf 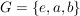 gibt es daher höchstens eine Gruppenstruktur: gibt es daher höchstens eine Gruppenstruktur:
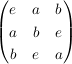
Man überzeugt sich leicht, dass dieses auch wirklich eine Gruppentafel ist.
m) Kleinsche Vierergruppe
n) Quaternionengruppe
Quelle: isbn3446130799
|