KettenregelSatz Kettenregel
f(x)=g(h(x))
("Innere Ableitung mal äußere Ableitung.")
Beispiele:
Beispiel 1: 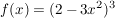
Es handelt sich hier um eine verkettete Funktion mit 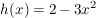 sowie sowie ![$ g(x) = [h(x)]^3 $ $ g(x) = [h(x)]^3 $](/teximg/4/4/00066244.png) . .
In diesem Fall könnte man die Klammer auch ausmultiplizieren und anschließend herkömmlich ableiten.
Dabei sollte man auf das gleiche Ergebnis kommen wie mit der Kettenregel.
Der Aufwand mit dieser Methode (ausmultiplizieren) wäre aber viel zu groß.
Zudem gibt es viele Funktionen, wo diese Methode nicht möglich ist (siehe Beispiel 2).
Zurück zum Beispiel...
innere Ableitung:
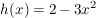 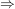 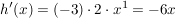
äußere Ableitung:
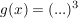 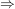 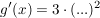
Bei der äußeren Ableitung ist uns zunächst völlig egal, was in der Klammer steht. Wir bilden zunächst ganz "normal" die Ableitung.
Das was in der Klammer steht (hier: 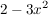 ), berücksichtigen wir erst mit der inneren Ableitung (in der Klammer könnte auch "APFELBAUM" stehen). ), berücksichtigen wir erst mit der inneren Ableitung (in der Klammer könnte auch "APFELBAUM" stehen).
Denn nun wenden wir die Kettenregel an:
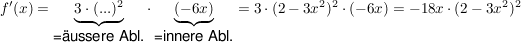
Beispiel 2: 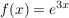
Wiederum verkettete Funktion mit h(x) = 3x sowie 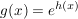 . .
Der (umständliche) Weg des Ausmultiplizierens funktioniert hier nicht!
innere Ableitung:
h(x) = 3x 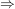 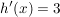
äußere Ableitung:
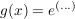 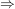 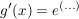 , da , da 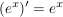
Kettenregel:

![Link auf "http://de.wikipedia.org/wiki/Kettenregel" [link]](/images/popup.gif) Kettenregel bei Wikipedia Kettenregel bei Wikipedia
weitere Regeln: siehe Ableitungsregel
| 