VerkettungDefinition Verkettete Funktion
Schule
Das Verketten von Funktionen g und h zu einer Funktion f entspricht dem Nacheinanderausführen der beiden Funktionszuordnungen.
Dabei darf die Schnittmenge der Wertemenge von h und der Definitionsmenge von g nicht leer sein.
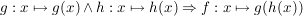
andere Schreibweise: 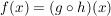 , gelesen: h vor g oder g nach h. , gelesen: h vor g oder g nach h.
Die Ableitung einer verketteten Funktion berechnet sich nach der Kettenregel.
Beispiel 1:
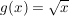 mit mit 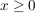
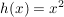 mit mit 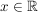
Berechne: 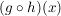
Dann gilt: 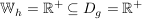
Folglich: 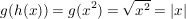 für für 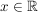
Beispiel 2:
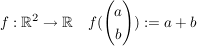 und und 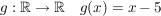
dann ist 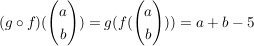 mit mit 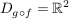 und und 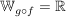 . .
Universität
| 