MonotonieuntersuchungWie untersuche ich die Monotonie einer Funktion?
Gib das Monotonieverhalten der Funktion f in Abhängigkeit von den Parametern a, b (ungleich 0) an.
a) f(x)= 
b) 
c) 
d) 
Monoton steigend in einem bestimmten Intervall ist eine Funktion genau dann, wenn ihre erste Ableitung in diesem Intervall größer gleich Null ist.
Analog dazu ist sie in einem Intervall genau dann monoton fallend, wenn ihre Ableitung in diesem Intervall nur Werte kleiner gleich Null annimmt.
Du musst also die Ableitungen der dir gegebenen Funktionen bestimmen und prüfen, wann diese positiv und wann negativ sind.
Dabei musst du das Ganze in Abhängigkeit von a durchführen.
Ich zeige dir mal an der ersten Funktion, wie das funktioniert.
Es ist 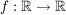 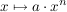 (ich nehme im Folgenden (ich nehme im Folgenden 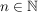 an). an).
Dann ist  . So, für . So, für  ist ist 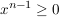 . .
Ist zudem  , so folgt , so folgt  für alle für alle  . .
Die Funktion ist also für  im Intervall im Intervall 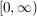 monoton steigend. monoton steigend.
Ist hingegen  , so folgt , so folgt  , die Funktion ist also im Intervall , die Funktion ist also im Intervall 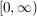 monoton fallend. monoton fallend.
Betrachten wir nun diejenigen 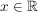 mit mit  und nehmen wir an, n sei ungerade, n-1 daher gerade. und nehmen wir an, n sei ungerade, n-1 daher gerade.
Dann ist 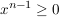 und, wie vorher, die Funktion f für und, wie vorher, die Funktion f für  im Intervall im Intervall ![$ (-\infty,0] $ $ (-\infty,0] $](/teximg/6/3/00147536.png) streng monoton steigend, für streng monoton steigend, für 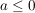 im Intervall im Intervall ![$ (-\infty,0] $ $ (-\infty,0] $](/teximg/6/3/00147536.png) streng monoton fallend. streng monoton fallend.
Ist hingegen n gerade und damit n-1 ungerade, so ist für  auch auch  ; dann ist f für ; dann ist f für 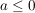 im Intervall im Intervall ![$ (-\infty,0] $ $ (-\infty,0] $](/teximg/6/3/00147536.png) monoton steigend, denn es ist monoton steigend, denn es ist 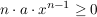 (denn es ist (denn es ist  und n-1 ungerade), für und n-1 ungerade), für  jedoch im Intervall jedoch im Intervall ![$ (-\infty,0] $ $ (-\infty,0] $](/teximg/6/3/00147536.png) monoton fallend, denn dann ist monoton fallend, denn dann ist  (denn es ist (denn es ist  ). ).
Für die anderen Funktionen sollte man selbst versuchen, die analogen Überlegungen anzustellen.
Bei Fragen kann man den ![Link auf "https://matheraum.de" [link]](/images/popup.gif) Matheraum befragen. Matheraum befragen.
| 