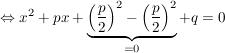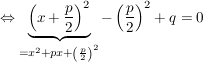PQFormelSatz pq-Formel
Die Lösung(en) einer quadratischen Gleichung der Form
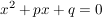 lauten für lauten für 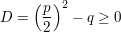 (dabei nennt man (dabei nennt man 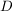 die Diskriminante der quadratischen Gleichung): die Diskriminante der quadratischen Gleichung):
und
In Kurzschreibweise:
;
für 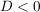 hat die quadratische Gleichung keine relle Lösung. hat die quadratische Gleichung keine relle Lösung.
Bemerkungen.
1.) Die pq-Formel ist ein Speziallfall der allgemeinen Lösungsformel für quadratische Gleichungen.
2.) In manchen Fällen führt der Satz von Vieta schneller zur gesuchten Lösung.
3.) 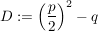 heißt Diskriminante. Es gilt damit: heißt Diskriminante. Es gilt damit:
Die Gleichung 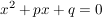 hat: hat:
- keine reelle Lösung, falls 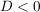
- genau eine reelle Lösung, falls 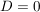
- genau zwei reelle Lösungen, falls 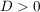 . .
4.) Darunter, dass die Ausdrücke definiert sind, versteht man hier, dass für die Diskriminante 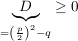 gilt. Es gilt nämlich: gilt. Es gilt nämlich:
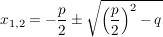
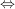
(I) 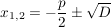
und 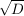 (bzw. (bzw. 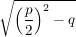 ) ist (im Reellen) nur für ) ist (im Reellen) nur für 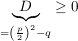 (wohl-)definiert! (wohl-)definiert!
(Wegen der Gleichung (I) gelten auch die Aussagen unter der Bemerkung 2.)!)
Beispiele.
1.) Wir suchen die reellen Lösungen der Gleichung  . .
Zunächst müssen wir uns um den Ausdruck vor dem 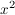 kümmern, d.h., wir dividieren die Gleichung durch kümmern, d.h., wir dividieren die Gleichung durch 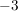 : :

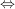
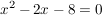 . .
Durch umschreiben erhalten wir die äquivalente Gleichung:
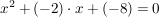 , d.h. hier ist , d.h. hier ist 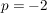 und und 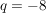 . .
Mit der p/q-Formel folgt also:
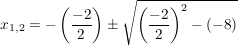
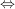
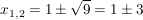
und damit haben wir zwei reelle Lösungen:
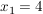 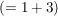 ; ;
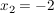 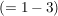 . .
Man beachte auch:
Die Diskriminante 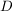 hatte hier den Wert hatte hier den Wert 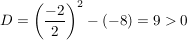 . .
Mit dem Satz von Vieta hätte man überlegt:
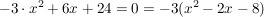
-8 = 2*(-4) und -2 = 2+(-4) 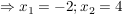
2.) Wir suchen die reellen Lösungen der Gleichung 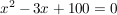 . .
Durch umschreiben erhalten wir die äquivalente Gleichung:
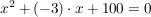 , d.h. hier ist , d.h. hier ist 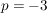 und und 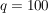 . .
Die Diskriminante 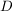 hat hier also den Wert: hat hier also den Wert:
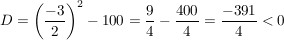 , also hat die Gleichung , also hat die Gleichung 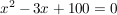 keine reelle Lösung. keine reelle Lösung.
3.) Wir suchen die reellen Lösungen der Gleichung 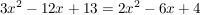 . .
Wir formen diese Gleichung etwas um:
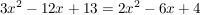
 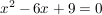
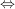
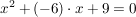 . .
Hier ist also 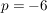 und und 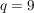 . .
Die Diskriminante hat hier den Wert:
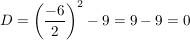 , also hat die Gleichung , also hat die Gleichung 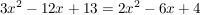 nur eine reelle Lösung. nur eine reelle Lösung.
Nach der p/q-Formel gilt:
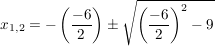
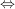
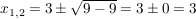 . .
Also ist 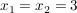 die einzige reelle Lösung der Gleichung die einzige reelle Lösung der Gleichung 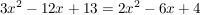 . .
(Dies kann man auch unmittelbar aus der Gleichung 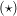 mittels der zweiten binomischen Formel ablesen!) mittels der zweiten binomischen Formel ablesen!)
Beweis.
Der Beweis wird mit einer allgemein durchgeführten quadratischen Ergänzung geführt:
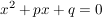
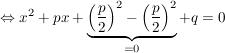
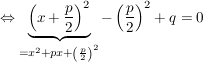
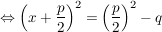 (Bemerkung: An dieser Stelle erkennen wir wegen (Bemerkung: An dieser Stelle erkennen wir wegen 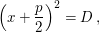
dass die Gleichung keine reelle Lösung im Falle 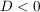 hat: hat:
Quadratzahlen von rellen Zahlen sind stets 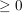 !) !)
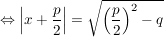
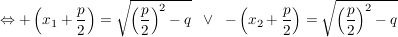
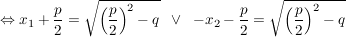
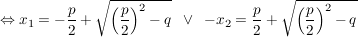
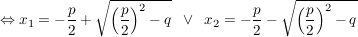
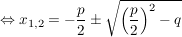
|