injektivVersion 3 von Fr 08.10.2004 um 18:40(Unterschied) ← Nächstältere Version | Aktuelle Version ansehen| Nächstjüngere Version → (Unterschied) Definitionen von injektiv, surjektiv, bijektiv
Seien D und Z nichtleere Mengen. Sei 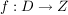 eine Funktion mit dem Definitionsbereich D und dem Zielbereich Z. eine Funktion mit dem Definitionsbereich D und dem Zielbereich Z.
Die Funktion f heißt:
- injektiv, falls für alle  mit mit 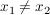 stets stets 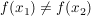 gilt gilt
(äquivalent dazu: f heißt injektiv, falls für alle  aus aus  stets auch stets auch 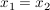 folgt .) folgt .)
- surjektiv, falls für alle 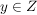 (mindestens) ein (mindestens) ein 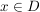 mit f(x)=y existiert mit f(x)=y existiert
(äquivalent dazu: f heißt surjektiv, falls f(D)=Z gilt. Hierbei ist f(D) der Bildbereich der Funktion f.)
- bijektiv, falls f sowohl injektiv als auch surjektiv ist.
Beispiele.
1.) Die Funktion 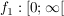  definiert durch definiert durch 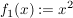 ist injektiv, nicht aber surjektiv. ist injektiv, nicht aber surjektiv.
2.) Die Funktion 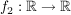 definiert durch definiert durch 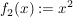 ist weder injektiv noch surjektiv. ist weder injektiv noch surjektiv.
3.) Die Funktion ![$ f_3:]-\infty;0[ $ $ f_3:]-\infty;0[ $](/teximg/6/1/00388716.png) 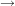 ![$ ]0;\infty[ $ $ ]0;\infty[ $](/teximg/7/1/00388717.png) definiert durch definiert durch 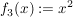 ist sowohl injektiv als auch surjektiv, also bijektiv. ist sowohl injektiv als auch surjektiv, also bijektiv.
4.) Die Funktion ![$ f_4:]0;\infty[ $ $ f_4:]0;\infty[ $](/teximg/9/1/00388719.png)  definiert durch definiert durch 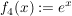 ist injektiv, jedoch nicht surjektiv. ist injektiv, jedoch nicht surjektiv.
5.) Die Funktion 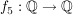 definiert durch definiert durch  ist injektiv und surjektiv, also bijektiv. ist injektiv und surjektiv, also bijektiv.
Bemerkungen.
1.) Wie man an den ersten drei Beispielen sieht, hängt es wesentlich von dem Definitions- bzw. dem Zielbereich ab, ob eine Funktion injektiv bzw. surjektiv ist. Das ergibt sich auch sofort aus den Definitionen.
2.) Genau dann, wenn eine Funktion bijektiv (also injektiv und surjektiv) ist, existiert eine Umkehrfunktion.
| 