Exponentialfunktion(allgemeine) Exponentialfunktion
Schule
... heißt eine Funktion mit dem Funktionsterm:
 mit 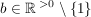
Ihr Definitionsbereich ist 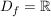 , ,
ihr Wertebereich ist 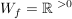 . .
Hat die Exponentialfunktion die Eulersche Zahl e als Basis,
so heißt sie natürliche Exponentialfunktion.
Ableitung der (allgemeinen) Exponentialfunktion
Man bildet den Differenzenquotienten:
durch Ausklammern ist der vordere Faktor von h unabhängig und kann im Grenzwert vorgezogen werden:
Jetzt braucht man "nur noch" für jedes  den hinteren Grenzwert zu bestimmen und kann dann die Ableitung an jeder beliebigen Stelle berechnen. den hinteren Grenzwert zu bestimmen und kann dann die Ableitung an jeder beliebigen Stelle berechnen.
Leider ist das ziemlich umständlich.
Darum sucht man nach einer Basis b, für die dieser Grenzwert gleich 1 ist; denn dann hat man eine ideale Situation:
Diese Zahl b gibt es! Sie liegt zwischen 2 und 3, genauer: ist die Eulersche Zahl e.
Bemerkung 1
Man kann für die Basis b Zahlen zwischen 0 und 1 zulassen: ![$ b \in ]0;1[ $ $ b \in ]0;1[ $](/teximg/1/1/00387611.png) . .
Allerdings gilt:  , ,
es gibt also für jedes ![$ b_1 \in ]0;1[ $ $ b_1 \in ]0;1[ $](/teximg/3/1/00387613.png) eine Funktion mit eine Funktion mit  , und daher reicht die Bedingung , und daher reicht die Bedingung  . .
Bemerkung 2
Soll man aus gegebenen Werten eine Exponentialfunktion bestimmen, so darf man die beiden Terme durch einander teilen, um einen Parameter zu eliminieren und anschließend den zweiten zunächst zu bestimmen:
Gesucht  , gegeben die Punkte auf dem Graphen: f(0)=1/3 und f(1)=32/3 , gegeben die Punkte auf dem Graphen: f(0)=1/3 und f(1)=32/3
Ansatz: 
Da 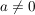 gilt (sonst wäre die Aufgabe sinnlos), kann man durch a kürzen und anschließend b bestimmen. gilt (sonst wäre die Aufgabe sinnlos), kann man durch a kürzen und anschließend b bestimmen.
Zum Schluss ermittelt man aus einer der beiden Gleichungen a und überprüft seine Rechnung mit Hilfe der anderen Gleichung.
Universität
siehe auch:
Logarithmusfunktion
![Link auf "http://de.wikipedia.org/wiki/Exponentialfunktion" [link]](/images/popup.gif) Exponentialfunktion bei Wikipedia Exponentialfunktion bei Wikipedia
![Link auf "http://de.wikipedia.org/wiki/Eulersche_Zahl" [link]](/images/popup.gif) Eulersche Zahl Eulersche Zahl
| 