Integralgeometrische Definition
Das bestimmte Integral benutzt man, um krummlinig begrenzte Flächenstücke zu berechnen.
Genauer:
Sei die Funktion f auf dem Intervall I stetig; sei 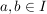 und f(x)>0 auf dem Intervall [a;b]. und f(x)>0 auf dem Intervall [a;b].
Dann ist die Maßzahl A der Fläche gesucht, die der Graph der Funktion f zwischen x=a und x=b mit der x-Achse einschließt.
Man unterteilt dazu das Intervall I in 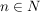 Teile mit der Länge Teile mit der Länge 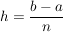 und bildet die Summe und bildet die Summe
also die Summe der Rechtecksflächen mit der Breite h und der Höhe 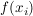 . .
Man kann dabei die 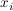 so wählen, dass sie die Mitte der Rechtecksseiten angeben. so wählen, dass sie die Mitte der Rechtecksseiten angeben.
Dann gilt:
Das Integralzeichen (= langgestrecktes S) deutet auf die Summenbildung,
das Symbol dx auf die Grenzwertbildung über die Variable x hin.
Die Funktion f(x) wird auch als Integrand oder Integrandenfunktion bezeichnet,
die Variable x als Integrationsvariable.
siehe auch: ![Link auf "http://www.geogebra.at/de/upload/files/dynamische_arbeitsblaetter/lwolf/oberuntersumme/oberuntersumme.html" [link]](/images/popup.gif) dynamische Veranschaulichung dynamische Veranschaulichung
andere Definition:
Wählt man die 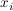 am linken Rand statt in der Mitte der Teilintervalle, am linken Rand statt in der Mitte der Teilintervalle,
so erhält man Rechtecke, deren linke obere Ecke auf dem Graphen liegen, die also vollständig unter dem Graphen liegen.
Dann bescheibt 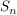 die Untersumme die Untersumme 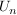 der Rechtecksflächen. der Rechtecksflächen.
Wählt man die 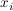 am rechten Rand statt in der Mitte der Teilintervalle, am rechten Rand statt in der Mitte der Teilintervalle,
so erhält man Rechtecke, deren rechte obere Ecke auf dem Graphen liegen, die also vollständig über dem Graphen liegen.
Dann bescheibt 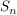 die Obersumme die Obersumme 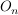 der Rechtecksflächen. der Rechtecksflächen.
siehe auch: Unter- und Obersumme
Man bildet wie oben die Grenzwerte für 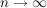 ; stimmen sie überein, ; stimmen sie überein,
so nennt man diesen gemeinsamen Grenzwert ebenfalls das bestimmte Integral der Funktion f.
Bemerkungen:
Wenn die Funktion f auch negative Funktionswerte besitzt, dann stimmt der Wert des Integrals nicht mehr mit dem Flächeninhalt überein, weil das bestimmte Integral dann die Differenz der Maßzahl des Flächeninhalts oberhalb und unterhalb der x-Achse angibt (orientierte oder signierte Flächen).
Zur Berechnung werden die Beträge der Einzelflächen zwischen den Nullstellen der Funktion f addiert.
Erstreckt sich eine Fläche bis ins Unendliche, dann muss sie, falls sie existiert, mithilfe der Kenntnisse über Grenzwerte bestimmt werden:
- Grundintegrale
Für eine Liste von einer Auswahl von Stammfunktionen siehe auch Grundintegrale
| 